A Survey of Mobile Guards in Art Galleries
Introduction
In 1973, in response to a request from Vasek Chvatal for an interesting geometric problem on which to work, Victor Klee responded with the problem of determining the minimum number of guards sufficient to guard an art gallery in the shape of a polygon with n walls. In 1975, Chvatal's publication of his result, [5], stimulated interest in the problem and its’ applications. The initial problem is closely related to some problems involving the decomposition of polygons. For example, since each guard in the gallery can see a star-shaped region, determining the number of guards necessary and sufficient to cover the polygon also determines the number of star-shaped regions necessary and sufficient to cover the polygon.
Many different variations of Chvatal’s Watchmen Problem have arisen. These variations include problems involving polygons with holes, guards that can see in a cone rather than the more often assumed omnidirectional visibility, and three-dimensional art galleries.
Many of the newer variations involve mobile guards. The earliest mobile guard variations involved guards patrolling the gallery along one wall or along line segments between vertices. The emphasis of these mobile guards were that every point of the gallery would be visible by a guard at some point in his patrol. More recently, attention has turned toward problems of pursuit and evasion in which a target tries to evade the guards. In these cases, the goal is often that of searching the gallery in such a way that an intruder must necessarily be detected.
It is mobile guards with which this paper is primarily concerned. Besides the obvious applications of searching buildings to detect intruders, other applications include air traffic control, military strategy, trajectory tracking, surgical applications, and computer-base arcade games.
Chvatal’s Watchman Theorem
In 1973, in response Victor Klee’s problem, Chvatal proved in [5] that n/3 guards will cover the interior of a polygon with n edges and that in some cases, n/3 guards are necessary for the task. In his original paper, he provided an example which required n/3 guards may be required to guard a polygon (see the diagram below). He then proved by induction that that n/3 guards are sufficient to guard any polygon.
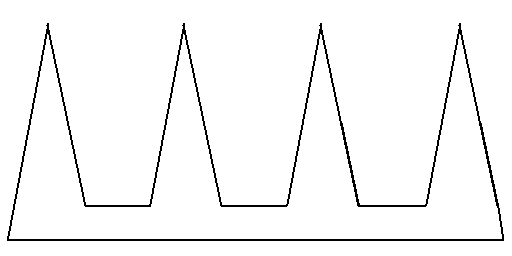
Figure 1: Example of gallery requiring n/3 guards
In [9], Steve Fisk provided a much simpler proof of the theorem. His proof first triangulates the polygon and then uses three colors to color the vertices so that each vertex in any given triangle is a different color from the other vertices. He then counts the number of vertices of each color and chooses the color which colors the fewest vertices. Thus, there can be no more than n/3 vertices of the chosen color. Placing a guard at each vertex of that color covers the polygon with no more than n/3 guards. It is important to note that this procedure is only guaranteed to find a cover of no more than n/3 guards, not the minimum cover.
One variation on the art gallery problems that seems to be completely unexplored is the question of multiple coverage of the gallery. If g guards are sufficient to cover a gallery with n walls, how many guards are necessary to provide multiple coverage of the gallery? That is, how many guards must be placed in the gallery so that at least m guards are visible from every point in the gallery? It is easy to find a gallery which can be covered by one guard if that guard is placed at a particular point, but if the guard is placed elsewhere, even arbitrarily close to the first guard, a portion of the gallery will be hidden from the guard. See Figure 2.
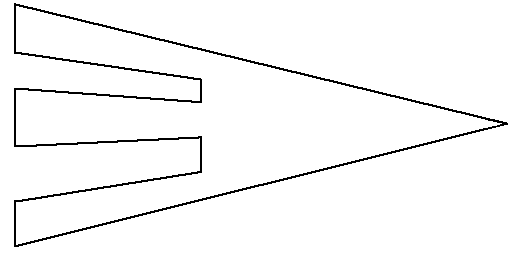
Figure 2: Example of polygon which requires four guards to provide double coverage. The entire polygon is only visible from the vertex.
Rectilinear Galleries
One common art gallery problem is that of orthogonal or rectilinear galleries. In a rectilinear gallery, any two edges are either parallel to each other or perpendicular to each other. Thus, an orthogonal coordinate system may be defined such that each edge is parallel to either the x-axis or the y-axis.
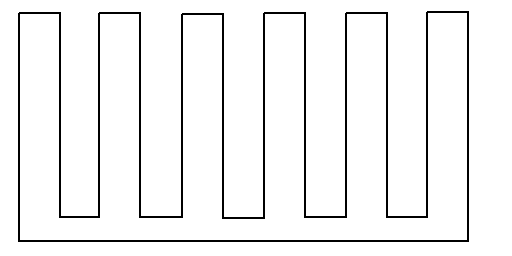
Figure 3: Example of rectilinear gallery requiring n/4 guards.
In [14], Kahn, Klawe, and Kleitman show that n/4 guards are sufficient to cover an art gallery in which all the edges are orthogonal. See Figure 3. The largest part of their proof involves showing that any orthogonal gallery may be partitioned into a set of convex quadrilaterals by drawing lines between vertices so that they do not intersect. This proof is similar to Fisk’s proof since once the gallery may be partitioned into convex quadrilaterals, the vertices may be colored by four colors. Placing a vertex guard at each vertex colored by any one color will cover the gallery. By choosing that color which colors the smallest number of vertices we know that there are no more than n/4 vertices of that color. Thus, n/4 guards are sufficient in an orthogonal or rectilinear gallery.
A rectangular gallery (Figure 4) is one in which the gallery is a rectangle subdivided into rectangular rooms with the stipulation that any two rooms which are adjacent has a door connecting them in which a guard may be placed. Since all points in a room are visible to a guard stationed in the doorway, each guard may maintain surveillance over two rooms simultaneously. In [7], Czyzowicz, Rivera-Campo, Santoro, Urrutia, and Zaks presented their results on rectangular galleries. They proved that in a rectangular gallery with n rooms, n/2 guards are sufficient to guard the gallery.
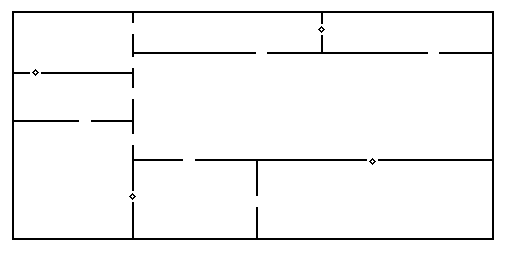
Figure 4: A Rectangular gallery with 8 rooms and 4 guards.
Czyzowicz and the others went on to consider an orthogonal gallery which has been decomposed into rectangular rooms. In this case, it is obvious that more than n/2 guards may be required. For example, consider a central rectangular room with a similar room on each side (see Figure 5). One guard may be situated so as to cover both the central square and one of the side rooms. However, each of the other side rooms will require an additional guard since no two side rooms share a common wall. Thus, we have five rooms requiring four guards. They showed that for a rectilinear gallery with v vertices and h holes that is decomposed into r rectangular rooms, (2r + v - 2h - 4) / 4 guards are sufficient.
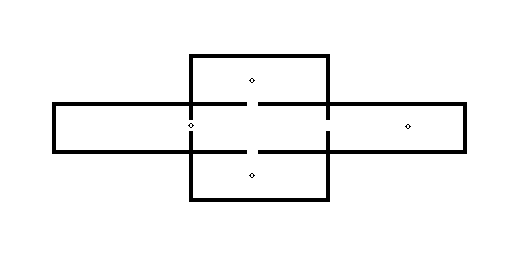
Figure 5: An orthogonal gallery with 5 rooms which requires 4 guards.
Mirrors
There are some interesting art gallery problems involving mirrors. [22] includes a brief discussion of these. Assuming the usual physical laws regarding reflection of light rays, the question is whether a polygon with mirrored edges may be lit be a single point source of light. While this is an open question for polygons, in the case of curved surfaces, a simple example shows a case in which there are areas which are not illuminated.
In this example, we have two half circles of different sizes with a common center. At that common center, a point source of light will fail to illuminate the two lobes on each side since each light ray is reflected straight back into the source. However, a point source of light placed elsewhere will be able to illuminate the entire area. A similar example may be used to show that there exist regions in which no single point source of light will illuminate the interior.
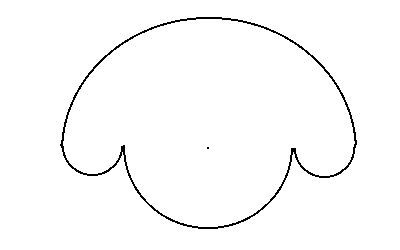
Figure 6: A point source of light fails to illuminate part of the area.
One open question by [23] concerns a forest composed of a finite number of disjoint circular trees whose boundaries are perfect mirrors. The question is whether there is any point from which the rays of a point light source will fail to escape to infinity.
Mobile Guards
Initially, mobile guards were constrained to patrol either along edges of the polygon or along straight lines wholly contained within the polygon. In the case of mobile guards patrolling along the edges of the polygon, the guards are known as "edge guards". If the guards patrol along straight line segments between vertices, the guards are known as "diagonal guards".
In 1981, Toussaint introduced the idea of having mobile guards in galleries. In particular, he was interested in the minimum number of edge guards necessary to guard the polygon. He conjectured that except for a small number of polygons, n/4 edge guards are sufficient to guard a polygon. Toussaint's original conjecture is still unproven.
O’Rourke [21] proved the more general result that the minimum number of mobile guards necessary and sufficient to guard a polygon is n/4 . His proof was a proof by induction similar to Chvatal’s original proof. He went further and showed that (3n+4)/16 mobile guards are necessary and sufficient to guard orthogonal polynomials.
Zoo-Keeper and Aquarium-Keeper Routes
Another form of mobile guards involves zoo-keeper routes and the related aquarium-keeper routes. In a zoo-keeper problem, a simple polygon P contains a set of convex polygons P1, ..., Pk. The problem is to find the shortest route which has at least one point in common with each of the interior polygons without going inside them. The zoo-keeper routes are intractable in general. [3], [4], and [20] discuss this problem in the special case in which the interior polygons each touch the outer polygon. In this case, the shortest path must travel either clockwise or counter-clockwise and may be found in O(n2) time and in O(n) if each polygon consists of a single edge. The algorithm first constructs an initial zoo-keeper's route and then adjusts the route up to O(n) times to determine the shortest route. When the interior polygons do not touch the boundary of the exterior polygon, the order in which the polygons are visited by the zoo-keeper's path becomes a major problem as there is no natural method to choose the order to visit the polygons.
The aquarium-keeper problem is to find the shortest path in a simple polygon which meets every edge of the polygon. There are two flavors of aquarium-keeper routes. If there are holes in the polygon, the holes are seen as obstacles to avoid, not as additional edges to visit. In polygons without holes, the aquarium-keeper route may be determined in O(n) time. If holes are present, the problem is more complex. When a point is given along the route, the fixed aquarium-keeper's route with holes, the route may be determined in O(n3) time. If no such point is given, determination of the route requires O(n4) time. When there are k aquarium keepers, the route determination requires O(nk+1) time.
Pursuit and Evasion Problems
Pursuit and evasion problems were apparently introduced by Leonardo Da Vinci. The usual pursuit and evasion problems are often expressed in the form of one animal trying to catch another, often by heading straight for the other animal. Such problems often have significant military applications when applied to questions of dogfights between aircraft.
In [13], Hoenselaers puts a new twist on the problem by considering the case of a dog chasing a hare which is traveling at relativistic speeds (near enough to the speed of light that relativistic effects become important). Usually, the idea is that the dog runs directly at the hare in an attempt to catch the hare. However, in the relativistic case, the dog is not running at the hare, but is instead running toward the point at which it sees the hare. Since the hare is running so fast, by the time the light from the hare has reached the dog, the hare has moved a significant distance. Hoenselaers considered two special cases of the problem. In the first of the two cases, the hare runs in a straight line and the dog is some distance from that line. In the second case, the hare runs in a circle and the dog is some distance from the circle.
Another kind of pursuit and evasion problem of more recent vintage is that of pursuit and evasion on a graph or grid. Typically, these are cops and robbers problems with one or more cops and one or more robbers. In [11], Goldstein and Reingold studied the complexity of problems in which k cops pursue and attempt to capture one robber on directed and non-directed graphs. They showed that the problem of determining whether k cops can capture a robber on an undirected graph with given initial positions is EXPTIME-complete. They also showed that the problem of determining that the k cops can capture the robber on a strongly connected directed graph (i.e. there is a directed path from each vertex in the graph to every other vertex in the graph) when the cops and then the robber choose their initial positions is also EXPTIME-complete. Some of the open problems on undirected graphs include:
- Which graph properties are necessary and sufficient for two or more cops to ensure capture of a robber?
- Given some number of cops, what is the smallest graph for which they are necessary and sufficient to capture a robber?
- For a given number of vertices on a graph, what is the maximum number of cops necessary to capture the robber?
- In a helicopter pursuit problem k cops fly in helicopters from vertex to vertex on the graph. The robber is allowed to move with infinite speed from vertex to vertex, but is constrained to move along the graph’s edges. What is the complexity of determining the number of cops necessary for a planar graph?
- The game of Annihilation is another game played on a graph. Each player has r different types of tokens each of which is constrained to move along a certain type of edge. That is, for a token of type i, it is constrained to move between vertices along a set of edges Ei. To make a move, a player selects a token of type i and moves it from one vertex to another along an edge in the set Ei. Whenever two tokens are located on the same vertex, both are removed from the graph and are no longer played. Is Annihilation EXPTIME-complete or PSPACE-complete in general?
Another pursuit and evasion game is discussed by Neufeld in [18]. In this version, the game is played on an n x m grid. The game uses one or more searchers with limited knowledge and visibility limited to edges in vertices in a straight line from the current position of the searcher. The game also includes a single fugitive with complete knowledge of the positions and strategies of the searchers. The fugitive’s top speed is one edge per unit of time while the searchers are allowed to move v edges per unit of time. The game is won by the searchers if one or more of the searchers can eventually see the fugitive. Otherwise, the fugitive wins. Two searchers can guarantee a win regardless of how slow they move along the grid. One way that they can do this by working together to systematically search the grid row by row from one side to the other.
Pursuit and Evasion in a Gallery
Interest in problems involving pursuit and evasion in galleries is very recent. The object is generally for one or more pursuit robots to capture or maintain surveillance of an evader. The capture of an invader is usually defined to be detection of the evader by one or more of the guards. The two primary questions which arise in relation to capturing evaders are:
- For a given problem, what is the minimum number of pursuers necessary to capture the evader?
- Can we efficiently compute a successful strategy to guarantee that the pursuers will capture the evader?
As in the pursuit and evasion problems on grids and graphs, it is helpful to perform the search in such a manner that the intruder cannot sneak past the searchers into a decontaminated area. However, there are cases in which this cannot be helped and areas must be searched again. If the number of searchers is too few, there will always be a strategy by which the intruder can sneak past the searchers and enter areas the searchers have already explored. [12] gives an example of a polygon in which part of the polygon must be decontaminated many times in the process of searching the polygon. In that case, adding an additional searcher could obviate the need for searching that area multiple times and suggests several questions that may be worth investigating:
- How many searchers are required to eliminate recontamination by the evader?
- Given a cost function for searching such as the product of the number of searchers and the time required for the search, when can we minimize the cost of searching by adding additional searchers?
In [17] and [12], the authors are concerned with using mobile robots to search a space for an unpredictable intruder whose position is unknown and who can move arbitrarily fast. They showed that the worse case bound on the minimum number of pursuers necessary is O(lg n) for a simply-connected free space and provide an example of a simply-connected space that requires W (lg n) pursuers.
They then present a complete algorithm for searching a two dimensional polygonal free space by a single robot. The algorithm decomposes the space in order to identify critical curves where edge visibility changes. This is important for the determination of those areas in the free space where it becomes possible for the evader to slip into a decontaminated area. A binary value is assigned to the edge of each cell in the decomposition to indicate whether or not the area has been decontaminated -- a value of "0" indicates the area is clear and a value of "1" indicates that the fugitive could be hidden behind there. When a solution has been found, every value has been changed to "0".
The cells built from the decomposition process are used to form a cell graph with the vertices representing the cells and the edges showing which cells are adjacent. Each cell is represented by a vertex in the graph. Two cells are connected on the graph if and only if they have a common edge in the free space. Since each cell corresponds to a set of visibility conditions, when moving from one vertex on the graph to another the information state has changed, i.e. new visibility conditions are added or old visibility conditions are removed. The cell graph is then used to construct a graph in the information quotient space which may then be searched to find a solution.
The authors feel that further work along this path along the following lines should be worth exploring:
- The use of approximation algorithms to find a solution within some bound of the optimal number of pursuers.
- Define a region of capture for the pursuers and define the task to be to capture the evader with one or more pursuers.
- Place bounds on the velocity of the evader.
- Study three dimensional free spaces.
- Limit the viewing angle of the pursuers.
- Use a cost function and study problems such as finding the evader in a minimum time.
Another recent problem in moving guards involves using a robot to maintain visibility of a target. In surgery, a somewhat autonomous robot could be used to maintain surveillance over the tools of the surgeon. For example, the surgeon may be unable to directly see what is doing and may rely on a video monitor to see the target area. Instead of requiring one of the operating room personnel to keep the camera aimed at the target, it may be more useful to have a computer perform that task.
In [16], LaValle, Gonzalez-Banos, Becker, and Latombe deal with this kind of problem. Thus, four conditions are assumed for this problem:
- The observer must maintain surveillance of the target.
- There are obstacles within the workspace which prohibit certain configurations of the target and observer.
- The workspace contains obstacles which interfere with the ability of the observer to watch the target area.
- The motion of the target is fully or partly known.
LaValle and the others first considered the case in which the target is predictable. Their algorithm breaks the time interval into K + 1 distinct points in time for which the position of the target is known and creates a space from the Cartesian product of the free space and the set of K + 1 integers from 1 to K + 1. For each k from 1 to K + 1, a standard sweep algorithm is used to map out the points in the free space visible from the target position. The values of a loss functional for each point in the visibility polygon would also be precomputed at this step. Then, at each stage, a cost-to-go function is computed which represents the accumulated cost from starting at the initial configuration and choosing the optimal action each step. From these cost-to-go calculations, the action that must be taken to achieve the next configuration are obtained.
The authors then consider the case of targets that are only partially predictable. A dynamic programming approach could be used for this case also, but the increased complexity led them to consider other approaches. They use feedback based on the current state to compute the control to be applied to move to the next state as in a standard control problem. They also point out that approximation or simplified strategies may be preferable for most real problems in order to cut down on the computational cost. One method they used was a probabilistic uncertainty model to maximize the probability that the target would still be in view at the next step. Another approach they studied was a method of maximizing the minimum time to escape. By using the maximum speed of the robot, they could calculate the minimum time required for the robot to reach the nearest edge of the area visible to the observer.
Some directions for future research in problems of maintaining visibility include:
- Approximation algorithms that can provide a solution within some bound of optimal. One example given is that of a random roadmap of the free space for problems in higher dimensions.
- Coordination of multiple observers and multiple targets.
- Imperfect information regarding the current configuration of the target.
- A reactive target that attempts to avoid the observer.
- Probabilistic speculations of the intentions of the target such as observing that when the target is seen along a particular route, it's destination is likely to be the usual destination it has along that route.
Another approach to pursuit and evasion was provided by Ichiro Suzuki and Masafumi Yamashita in [26]. They considered the problem of using a mobile searcher to find a mobile intruder in a simple polygon with a limitation placed on the searcher that the searcher could only see along rays in k directions at one time by the use of k flashlights. They were interested in a particular classification of polygons for which a searcher with two flashlights is as capable of finding the evader as a ¥ -searcher (i.e. a searcher who can see in all directions simultaneously). These polygons are termed hedgehogs and have a single convex body with thin hooked pins.
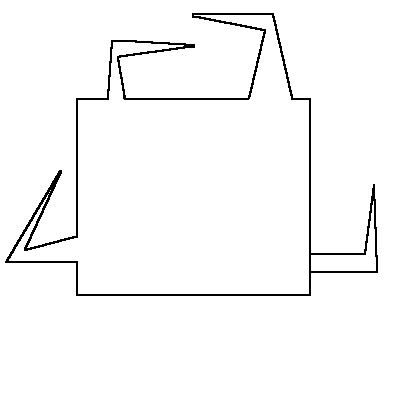
Figure 7: A Hedgehog Polygon
Suzuki and Yamashita showed that if a polygon with n sides is searchable by an ¥ -searcher, then it is searchable by a ( n/2 +1)-searcher.
Two points, x and y, are called separable by a point, z, if the shortest path between x and y contains no points which are visible by z. Three points x, y, and z are called mutually separable if no two points of the three are separable by the third. In the case of a 1-searcher, Suzuki and Yamashita showed that for any polygon which is searchable by a 1-searcher, if x, y, and z are points in the polygon, x, y, and z are mutually nonseparable. In a hedgehog with three pins, the tips of the three pins are mutually separable and thus a 1-searcher is insufficient.
The authors conjecture that any ¥ -searcher polygon is 2-searchable. In the case of hedgehogs, they show that this is indeed true. It would be interesting to find a polygon which is k-searchable, but is not (k-1) searchable for some 3 £ k £ n/2 + 1.
Conclusion
The field of searching art galleries with mobile guards is quite new and open problems exist in abundance. Many of these problems (probably most of the interesting problems) are intractable.
Joseph O'Rourke provides a list of thirty eight open problems involving different aspects of art gallery theorems in [23]. Many of the problems involving The problems he listed involving mobile guards all specifically involve edge guards:
- How many edge guards are needed to cover the interior of a simple polygon of n edges? For n> 11, the best lower bound is currently n/4 and the best upper bound is 3n/10 .
- How many edge guards are necessary to cover the interior of a star-shaped polygon. It has already been shown by Toussaint that n/5 are necessary.
- Are n/4 edge guards sufficient to cover a star-shaped polygon with n vertices?
Other open problems include:
- Find a polynomial-time algorithm to find a shortest watchman route in a simple polygon without a specified starting point.
- Find a polynomial-time algorithm to find a shortest watchman path in a polygon.
- Characterize those polygons for which one mobile guard is sufficient.
Bibliography
[1] S. Carlsson and H. Jonsson, "Computing a Shortest Watchman Path in a Simple Polygon in Polynomial Time",
Carlsson and Jonsson are concerned with the question of finding the shortest watchman path in a polygon. Their motivation is to design a rescue robot which can search a burning building for persons and objects. They first consider the shortest path that visits all the vertices of the polynomial. They then consider the aquarium-keeper's problem, the shortest path that visits every edge of the polygon and present an algorithm to compute the shortest aquarium-keeper's path. Finally, they present the algorithm for the shortest watchman path which requires O(n12) time.
[2] S. Carlsson and H. Jonsson, "Guarding a Treasury".
Carlsson and Jonsson investigate the problems of guarding a treasury. That is, given a set of points within a polygon which need guarding, determine a location at which to place a guard so that the value of the treasures which the guard can see is maximized.
[3] W.-P. Chin, "The Zookeeper Route Problem", Information Sciences 63 (1992), pp 245-259.
Chin considers the problem of {S,T} routes in which a path is to be found in a polygon containing a set of points S and a set of points T. The S points are sights that must be visible from at least one point in the route while the T points are threats must never be visible from any point along the route. If the threats are enclosed in polygons, the problem becomes the zoo-keeper route problem. By restricting these polygons to be attached to the edges of the outer polygon, he finds an algorithm for finding the shortest such path and shows that it is unique. The time complexity of his algorithm is
.
[4] W.-P. Chin and S. Ntafos, "Optimum Zoo-Keeper Routes", Congressus Numerantium 58 (1987) pp 257-266.
Chin and Ntafos present an algorithm for the purpose of finding a shortest route that visits a set of convex polygons attached to the interior of the boundary of a simple polygon. Since the polygons are attached to the interior, the search for solutions may be restricted to paths which run clockwise or counter-clockwise from polygon to polygon.
[5] V. Chvatal, "A Combinatorial Theorem in Plane Geometry", Journal of Computorial Theory (B) 18 (1975), pp 39-41.
The original paper on art gallery problems. Vasek Chvatal gives an example in which n/3û guards are necessary to cover a polygon and presents a proof by induction that n/3 guards are sufficient to cover a polygon.
[6] P. Colley, H. Meijer, and D. Rappaport, "Motivating Lazy Guards".
This paper deals with the lazy guard problem which is stated: given a polygon, choose a minimum number of points such that every point in the polygon is visible from at least one point of any path connecting those points. A polygon which can be guarded in this manner with k stations is called lazy k guardable. The lazy guard problem for polygons with holes is shown to be NP-hard.
[7] J. Czyzowicz, E. Rivera-Campo, N. Santoro, J. Urrutia, and J. Zaks, "Guarding Rectangular Art Galleries", TR-89-27, University of Ottawa.
Czyzowicz, Rivera-Campo, Santoro, Urrutia, and Zaks present their results on rectangular art galleries. They show that é n/2ù guards are sufficient to guard a gallery having n rooms. Furthermore, they prove that in a gallery having v vertices and r rectangular rooms with h holes, é (2r+v-2h-4)/4ù guards are sufficient to guard all the rooms.
[8] H. Edelsbrunner, J. O’Rourke, and E. Welzl, "Stationing Guards in Rectilinear Art Galleries", Computer Vision, Graphics, and Image Processing 27 (1984), pp 167-176.
Edelsbrunner, O'Rourke, and Welzl considered the problem of stationing guards in rectilinear art galleries . Their algorithm partitions the polygon into L-shaped pieces and places a guard in each. For n vertices, the algorithm runs in O(n log n) time.
[9] S. Fisk, "A Short Proof of Chvatal’s Watchman Theorem", Journal of Combinatorial Theory, Series B 24 (1978) pg 374.
Steve Fisk presents a substantially shorter proof of Chvatal’s Watchman Theorem.
[10] L. P. Gewali and S. Ntafos, "Watchman Routes in the Presence of a Pair of Convex Polygons (Extended Abstract)"
This paper deals with the problem of finding the shortest watchman route for which the exterior of a set of polygons is visible from at least one point along the route. Note that these polygons are located in the plane and not inside another polygon as in zoo-keeper routes. They present an O(n2) algorithm for finding such a route with a total number of n edges.
[11] A. S. Goldstein, and E. M. Reingold, "The complexity of pursuit on a graph", Theoretical Computer Science 143 (1995) 93-112.
This paper studies pursuit problems on directed and undirected graphs.
[12] L. J. Guibas, J.-C. Latombe, S. M. LaValle, D. Lin, and R. Motwani, "A Visibility-Based Pursuit-Evasion Problem", Submitted to the International Journal of Computational Geometry and Applications.
This paper is very similar to [16], but it does cover more material on computing the number of searchers required. For example, they show that there are free spaces which require the number of searchers to be
where h is the number of holes and n is the number of edges. They also present an example of a free-space which requires only one searcher, but requires W (n) recontaminations.
[13] C. Hoenselaers, "Chasing Relativistic Rabbits", General Relativity and Gravitation, Vol 27, No 4, 1995.
Hoenselaers looks at the classical problem of pursuit and evasion and adapts it to a relativistic version in which the pursuer aims at the point he sees the target, not at the actual point the target is located.
[14] J. Kahn, M. Klawe, and D. Kleitman, "Traditional Galleries Require Fewer Watchmen", SIAM J. Alg. Disc. Meth., Vol 4, No. 2, June 1983, pp 194-206.
This paper studies the placement of guards in orthogonal polygons. Whereas a general polygon requires at most n/3û guards, they show that if the polygon is rectangular, no more than n/4 guards are needed. Most of the paper is concerned with the quadrilateralization of the polygon.
[15] D. T. Lee and A. K. Lin, "Computational Complexity of Art Gallery Problems", IEEE Transactions on Information Theory, Vol. IT-32, No 2, March 1986, pp 276-282.
The authors studied the computational complexity of the art gallery problem. Their primary interest was the problem of determining the minimum number of vertex guards that can see an n-wall simply connected art gallery. This was shown to be NP-hard. Their proof can be modified to show that the problems of determining the minimum number of edge guards and the minimum number of point guards in a simply connected polygonal region are also NP-hard. Finally, they showed that the problem of decomposing a simple polygon into a minimum number of star-shaped polygons such that their union is the original polygon is also NP-hard.
[16] S. M. LaValle, H. H. Gonzales-Banos, C. Becker, and J.-C. Latombe, "Motion Strategies for Maintaining Visibility of a Moving Target" , Submitted to the 1997 IEEE International Conference on Robotics and Automation.
LaValle, Gonzales-Banos, Becker, and Latombe considered the computation of robot motion strategies that maintain visibility of a moving target in a cluttered workspace. They considered both the case of a predictable target and an unpredictable target. For the predictable target, they presented an algorithm to maintain visibility while taking into account other considerations such as maintaining a specified distance between the target and the observer. They also considered the case of an unpredictable target and looked at two approximation strategies: maximizing the probability of future visibility and maximizing the minimum time in which the target can escape.
[17] S. M. LaValle, D. Lin, L. J. Guibas, J.-C. Latombe, and R. Motwani, "Finding an Unpredictable Target in a Workspace with Obstacles", Submitted to the 1997 IEEE International Conference on Robotics and Automation.
LaValle, Lin, Guibas, Latombe, and Motwani are interested in algorithms which may be used by mobile robots to search a gallery for an intruder robot and guarantee their success.
[18] S. W. Neufeld, "A pursuit-evasion problem on a grid", Information Processing Letters 58 (1996) pp 5-9.
Neufeld is concerned with the cops and robber game played on an m ´ n grid. The cops have visibility only along the rows and columns of the grid and no nothing about the robber's location. The robber, on the other hand, knows the location and strategy the cops are using. The main question with which the author is concerned is with the minimum speed by which the searcher can force a win.
[19] B. J. Nilsson, "Guarding Art Galleries: Methods for Mobile Guards", Thesis, Department of Computer Science, Lund University, 1994
Given a robot patrolling along a watchman route in an art gallery, Nilsson is concerned with the problem of determining from which points the robot must use its' sensors to see the polygon. He then goes on to the more common approach of a robot that is always watching and tries to minimize the length of the route. He discusses the shortest fixed watchman route, one point along the route is given, and notes that the best known current algorithm by Tan and Hirata requires O(n2) by the use of divide and conquer. The shortest floating watchman route is much more complex. In this route, there is no set point through which the route must pass. His algorithm requires O(n4) worst case running time. He then looks at the shortest watchman's routes for spiral, alp, and histogram polygons.
[20] S. Ntafos and M. Tsoukalas, "On K Aquarium-Keeper and Zoo-Keeper Routes", Congressus Numerantium, 83 (1991), pp 25-32.
Ntafos and Tsoukalas consider zoo-keeper routes and aquarium-keeper routes. They present an algorithm for finding the shortest aquarium-keeper routes in polygons with holes. They also look at a version in which there are k keepers.
[21] J. O’Rourke, "Galleries Need Fewer Mobile Guards: A Variation on Chvatal’s Theorem", Geometriae Dedicata 14 (1983) pp 273-283.
O'Rourke considers the question of mobile guards patrolling fixed line segments in the interior of polygons and shows that for n³ 4, n/4 guards are sufficient and sometimes necessary.
[22] J. O’Rourke, "Art Gallery Theorems and Algorithms", Oxford University Press, London, New York, 1987.
This is the classic book on the subject of art gallery theorems. The author discusses the original art gallery theorem and the triangulation and quadrilateralization of polygons as well as art galleries with holes. He briefly discusses other problems such as the art gallery problem in three dimensions and questions regarding illumination of the interior of the gallery by a point source light.
[23] J. O’Rourke, "Combinatorics of Visibility and Illumination: 38 Open Problems", Department of Computer Science, Smith College.
This is a recent list of thirty eight open problems involving art galleries. They cover art gallery theorems, exterior illumination, floodlights, polygon vertex visibility graphs, computational complexity, segment visibility graphs, rectangle visibility graphs, visibility graphs in 2 1/2 D and 3D, and point visibility graphs.
[24] T. Shermer, "Recent Results in Art Galleries", TR90-10, Computing Science, Simon Fraser University, 1990.
Thomas Shermer surveys recent results in field of art galleries. He concerns himself mainly with the standard art gallery theorems and visibility questions.
[25] K. Sugihara, I. Suzuki, and M. Yamashita, "The Searchlight Scheduling Problem", SIAM J Comput. Vol 19, No 6, pp 1024-1040, December 1990.
Sugihara, Suzuki, and Yamashita considered the problem of searching for a mobile robber in a simple polygon. In this variation, the searchers are stationary and equipped with searchlights whose direction can be changed continuously. Their primary task is to devise a schedule for aiming the searchlights so that the mobile robber will be detected.
[26] I. Suzuki and M. Yamashita, "Searching for a Mobile Intruder in a Polygonal Region", SIAM J. Comput., Vol 21, No 5, pp 863-888, October 1992.
This paper deals with the question of searching for a mobile intruder in a polygon in which the searchers see only in k directions at a time in a manner similar to flashlights. They introduce a class of polygons for which a searcher with two flashlights is just as capable of finding an intruder as a searcher with a point light source. These polygons, called hedgehogs, are simple polygons consisting of a convex body and a set of narrow hooked pins. A requirement placed on the pins is that they must be sufficiently narrow and oriented such that no point in the entrance of a pin is visible from the tip of any other pin.